| |
Pourquoi un miroir n'inverse-t-il pas le haut et le bas ? |
| |
 |
Par Franck Stevens
Article mis en ligne le 04/07/13 |
C'est bien connu, la façon dont vous vous voyez dans un miroir ne correspond donc pas à la façon dont les autres vous voient : votre mèche qui tourne vers la gauche semble tourner vers la droite dans le miroir. Mais si un miroir inverse la gauche et la droite, pourquoi le haut et le bas ne sont-ils pas aussi inversés ?

Votre image dans un miroir est inversée horizontalement : le texte sur vos vêtements y est illisible !
Image : Sciences Claires

Votre image dans un miroir est inversée horizontalement : le texte sur vos vêtements y est illisible !
Image : Sciences Claires
Si vous n'êtes pas convaincu, mettez-vous face à un miroir et levez la main gauche. Vous constaterez que votre image dans le miroir lève sa main droite ! Par contre, même dans votre reflet, votre tête est bien en haut et vos pieds sont bien en bas, comme c'est le cas en réalité. Comment expliquer ce paradoxe apparent ?
Cela n'est pas d√Ľ √† la forme du miroir, comme ce serait le cas si vous vous regardiez dans une cuiller (ou un miroir concave de fa√ßon g√©n√©rale) : dans ce cas-l√†, il y a bien inversion du haut et du bas. Or, ici, le miroir est parfaitement plat.
Autre chose étrange : quand vous êtes debout devant votre miroir, il semble échanger votre main gauche et votre droite… mais si vous vous couchez devant lui, vous constaterez qu'il n'échange pas votre tête et vos pieds ! Par contre, il semble toujours bien échanger votre main gauche et votre main droite, alors que celles-ci sont désormais en haut et en bas.
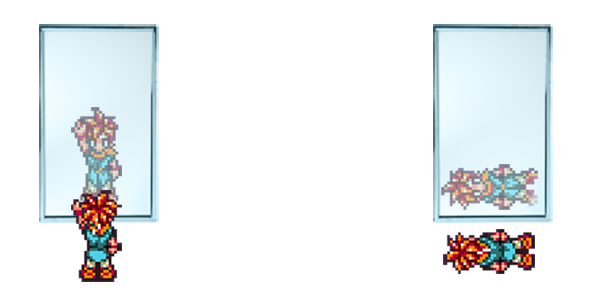
Le miroir semble √©changer votre main gauche et votre main droite‚Ķ et ce, quel que soit le sens o√Ļ vous vous mettez ! Par contre, vous aurez beau faire, il n'√©changera jamais votre t√™te et vos pieds.
Image : Sciences Claires

Le miroir semble √©changer votre main gauche et votre main droite‚Ķ et ce, quel que soit le sens o√Ļ vous vous mettez ! Par contre, vous aurez beau faire, il n'√©changera jamais votre t√™te et vos pieds.
Image : Sciences Claires
Comment expliquer cela ? En r√©alit√©, il est un peu abusif de dire que le miroir √©change la gauche et la droite. Certes, lorsque vous levez votre main gauche, votre reflet l√®ve sa main ¬ę droite ¬Ľ‚Ķ mais cette main est celle qui est situ√©e √† gauche du miroir, juste en face de votre main gauche. Il s'agit donc bien du reflet de votre main gauche, mais vous aurez tendance √† la consid√©rer comme une main ¬ę droite ¬Ľ que parce que vous vous imaginez √† la place du reflet.
Cependant, la différence fondamentale entre le reflet et vous, c'est la direction dans laquelle vous regardez. Fixez-vous un point de repère absolu (par exemple le nord) et vous constaterez que votre reflet regarde dans la direction opposée : vous regardez vers le nord et lui vers le sud !
Or, la gauche et la droite sont des directions relatives, qui d√©pendent de la direction vers laquelle vous regardez : un objet qui se trouve sur votre gauche se retrouvera sur votre droite si vous faites un demi-tour sur vous-m√™me. Ce n'est par contre pas le cas du haut et du bas, qui ne d√©pendent pas de la direction o√Ļ vous regardez, ni des points cardinaux comme le nord, le sud, l'est et l'ouest.
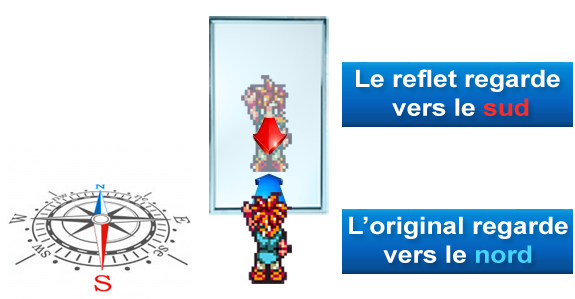
Lorsque vous regardez vers le nord, votre reflet regarde vers le sud. Si vous levez votre main gauche, c'est-√†-dire celle qui est vers l'ouest, le reflet l√®ve sa main ¬ę droite ¬Ľ‚Ķ qui est √©galement celle qui est vers l'ouest !
Image : Sciences Claires

Lorsque vous regardez vers le nord, votre reflet regarde vers le sud. Si vous levez votre main gauche, c'est-√†-dire celle qui est vers l'ouest, le reflet l√®ve sa main ¬ę droite ¬Ľ‚Ķ qui est √©galement celle qui est vers l'ouest !
Image : Sciences Claires
En somme, le miroir n'échange pas réellement la gauche et la droite : il serait plus correct de dire qu'il échange l'avant et l'arrière. Mathématiquement, il s'agit d'une symétrie orthogonale par rapport au plan du miroir.
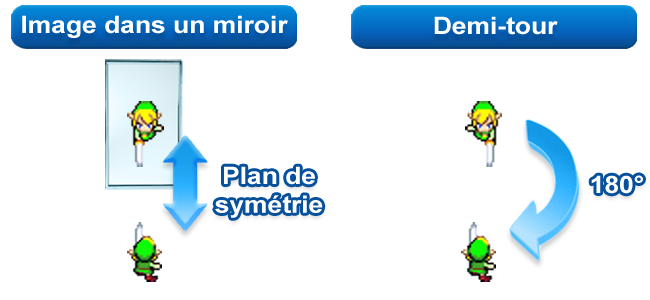
Le miroir a l'effet d'une sym√©trie orthogonale (√† gauche), ce qui ne m√®ne pas au m√™me r√©sultat qu'un demi-tour (√† droite). Le personnage tient toujours son √©p√©e dans sa main gauche, sauf dans le reflet du miroir, o√Ļ il semble la tenir dans sa main droite.
Image : Sciences Claires

Le miroir a l'effet d'une sym√©trie orthogonale (√† gauche), ce qui ne m√®ne pas au m√™me r√©sultat qu'un demi-tour (√† droite). Le personnage tient toujours son √©p√©e dans sa main gauche, sauf dans le reflet du miroir, o√Ļ il semble la tenir dans sa main droite.
Image : Sciences Claires
Le ¬ę paradoxe du miroir ¬Ľ n'en est donc pas vraiment un‚Ķ si l'on prend le temps de bien y r√©fl√©chir !
Pour en savoir plus |
- Richard Feynman Mirror (Youtube) (en anglais)
Interview du physicien Richard Feynman expliquant le problème et sa solution
Copyright et licence |
- Les images et vidéos utilisées sur cette page sont la propriété de leurs auteurs respectifs
- Le texte est quant à lui la propriété intellectuelle de Franck Stevens
- Vous avez le droit de reproduire ce texte à des fins non commerciales et de le modifier, à condition d'indiquer clairement vos modifications, de mentionner explicitement le nom de l'auteur et d'inclure un lien en dur vers cette page, selon les termes de la Licence Creative Commons Attribution - Pas d’Utilisation Commerciale - Partage dans les Mêmes Conditions 3.0 non transposé.

Classement |
 Auteur(s) : Franck Stevens
Auteur(s) : Franck Stevens
 Catégorie : Question
Catégorie : Question
 Discipline(s) : Physique, Optique
Discipline(s) : Physique, Optique
Voir les pages... |











